Thermal Neutron Capture
The neutron-capture reaction is fundamental for identifying and analyzing the γ-ray spectrum from an unknown assembly because it provides unambiguous information on the neutron-absorbing isotopes. Nondestructive-assay applications may exploit this phenomenon passively, for example, in the presence of spontaneous-fission neutrons, or actively where an external neutron source is used as a probe. There are well-known gaps in the Evaluated Nuclear Data File (ENDF) libraries corresponding to neutron-capture γ-ray data that otherwise limit transport-modeling applications, e.g., the lead isotopes [Hur17]. In this project, we describe how new thermal neutron-capture data are being used to improve information in the neutron-data libraries relevant to nonproliferation applications; in particular for primary γ rays that originate at the neutron-separation energy where the observed experimental data are frequently at odds with the data in ENDF. We address this problem by providing new experimentally-deduced partial and total neutron-capture reaction cross sections and then evaluate these data by comparison with statistical-model calculations. Recent examples of our work in this area include: 139La(n,γ) [Hur19], 180W(n,γ) [Hur15], 182,183,184,186W(n,γ) [Hur14], and 185Re(n,γ) [Mat16].
Highlights
In addition to the provision of new absolute neutron-capture γ-ray cross-section data to help guide the development of ENDF libraries, especially in the high-Eγ "primaries" regime, radiative neutron-capture measurements have contributed to developments in several other aspects of basic and applied nuclear physics. A few highlights are discussed below.
Methodology Development
An analytical procedure has been developed for the determination of the effective thickness of non-uniform irregular samples exposed to a flux of thermal neutrons [Hur15b]. Precise knowledge of the thickness, corresponding to the active volume of the bulk sample, is required to adequately correct for attenuation of γ rays due to photoelectric absorption within the sample itself. Such procedures are especially required for low-energy γ rays (Eγ) in high-density (ρ) materials. Using this methodology, the attenuation is determined by integrating the exponential-attenuation law Iγ/I0 = exp(-μγ x) over the sample depth x,
$$ \frac{I_{\gamma}}{I_{0}} \int\limits_{x=0}^{x=t} dx = \int\limits_{x=0}^{x=t} \exp \left( \frac{-\rho \left(\frac{\mu_{\gamma}}{\rho}\right)_{E_{\gamma}} x}{\cos\theta} \right) dx, $$to arrive at the Eγ- and thickness-(t) dependent expression for the photon attenuation given by
$$ \frac{I_{\gamma}(E_{\gamma},t)}{I_{0}} = \frac{\cos\theta}{\rho \left(\frac{\mu_{\gamma}}{\rho}\right)_{E_{\gamma}} t} \left[ 1 - \exp \left( \frac{-\rho \left(\frac{\mu_{\gamma}}{\rho}\right)_{E_{\gamma}} t}{\cos\theta} \right) \right], $$where θ is the angle of the sample face relative to the detector and μγ/ρEγ are the Eγ-dependent mass-attenuation coefficients from XMuDat [Xmu98]. The software (C++) developed to calculate the attenuation according to this prescription, including the complete library of mass-attenuation coefficients from XMuDat, can be downloaded from here.
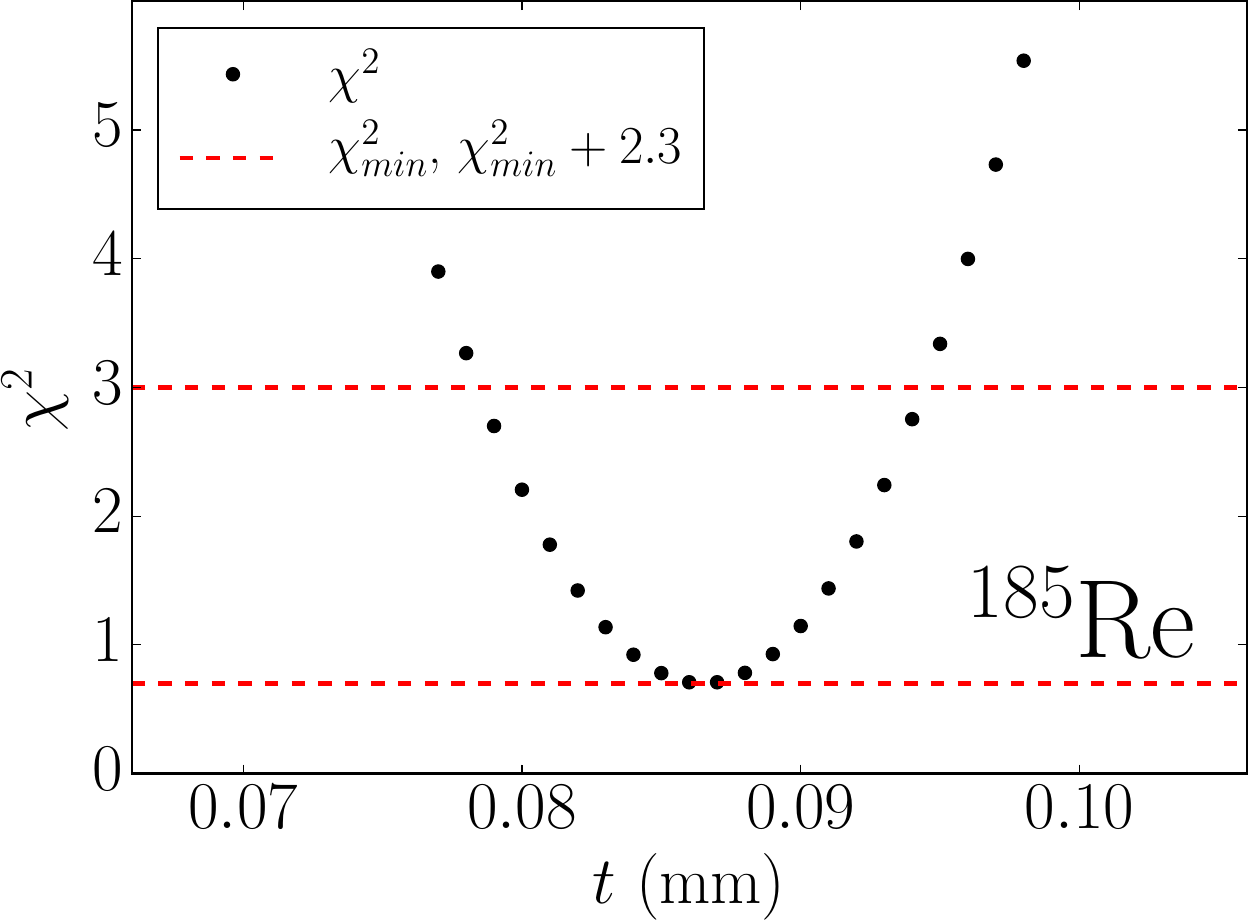
Figure 1 Plot of the global χ2 as a function of the 185Re effective-sample thickness. The upper and lower dashed lines define the χ2min + 2.3 range of values consistent with the 1σ range (68.3% confidence level) for a minimization based on a two-parameter adjustment [Ber12]. Taken from Ref. [Mat16].
Provided that we have a suitable set of well-known standard partial γ-ray cross sections σγS to compare with the measured yields YγC, corrected for efficiency and attenuation at the a priori assumed t, the corresponding ratio σγS/YγC should be a constant for any γ ray:
$$ \frac{\sigma_{\gamma_{1}}^{S}(E_{\gamma_{1}})}{Y_{1}^{C}(E_{\gamma_{1}})} = \frac{\sigma_{\gamma_{2}}^{S}(E_{\gamma_{2}})}{Y_{2}^{C}(E_{\gamma_{2}})} = \frac{\sigma_{\gamma_{3}}^{S}(E_{\gamma_{3}})}{Y_{3}^{C}(E_{\gamma_{3}})} = \dots $$or, in general terms, we may define the ratio
$$ R_{i}(E_{\gamma_{i}}) = \frac{\sigma_{\gamma_{i}}^{S}(E_{\gamma_{i}})}{Y_{i}^{C}(E_{\gamma_{i}})} = {\rm const}. $$Thus, by iterating over a suitable range of t values, a χ2 minimization can then be performed to find the best-fit value t to reproduce the observed attenuation. Because Ri(Eγi) measurements are correlated we need to use a covariance matrix to perform the minimization
$$ \chi^{2} = ({\bf R_{w}} - {\bf R}) {\bf V}^{-1} (\widetilde{\bf R_{w}} - \widetilde{\bf R}), $$where R is vector of N elements corresponding to the ratios R1(Eγ1), R2(Eγ2), ... RN(EγN). Each element in the Rw vector of equivalent length corresponds to the calculated average of all Ri(Eγi) determined at the assumed t. The transposed vectors are denoted as R̃ and R̃w, respectively. In the covariance analysis, we also treat the correlation coefficient rij as an adjustable parameter, where the N x N covariance matrix may be represented as
$$ V = \left( \begin{array}{cccc} r_{11} \Delta_{R_{1}}\Delta_{R_{1}} & r_{12} \Delta_{R_{1}}\Delta_{R_{2}} & \dots & r_{1N} \Delta_{R_{1}}\Delta_{R_{N}} \\ r_{21} \Delta_{R_{2}}\Delta_{R_{1}} & r_{22} \Delta_{R_{2}}\Delta_{R_{2}} & \dots & r_{2N} \Delta_{R_{2}}\Delta_{R_{N}} \\ \vdots & \vdots & \ddots & \vdots\\ r_{N1} \Delta_{R_{N}}\Delta_{R_{1}} & r_{N2} \Delta_{R_{N}}\Delta_{R_{2}} & \dots & r_{NN} \Delta_{R_{N}}\Delta_{R_{N}} \end{array} \right). $$This methodology has been successfully adopted in studies of 182W(n,γ), 186W(n,γ) [Hur14, Hur15b], 185Re(n,γ) [Mat16], 187Re(n,γ) [War21], and 139La(n,γ) [Hur19]. Figure 1 illustrates a representative example in the case of 185Re(n,γ) where an effective sample thickness t = 0.86(8) mm [Mat16] was deduced.
Improving nuclear structure data (I): Jπ determination
Spin J and parity π are amongst some of the most important quantum mechanical properties of the nucleus. Precise knowledge of these decay-scheme properties are key to reliable nuclear structure and reaction-model calculations. Radiative thermal neutron-capture reactions provide a direct probe to assess these quantities. In our work on 186W(n,γ) [Hur14] we were able to confirm several Jpi assignments for levels below 900 keV in the residual compound nucleus, 187W, by comparison of the measured experimental partial γ-ray cross-section data with statistical-model calculations. However, the currently adopted 7/2+ and 11/2+ assignments for the 884.1- and 410.1-keV levels [Bas09], respectively, are tentative assignments and are at odds with the present cross section measurements and statistical-model predictions, as shown in Fig. 2a. Lowering the value of J by precisely one unit of angular momentum for each assignments reveals far better agreement with the statistical model, as shown in Fig. 2b. Furthermore, because a rotational cascade is built upon the 410.1-keV state, all Jπ values for the corresponding cascade members are impacted with associated Δ J = -1 changes.
Figure 2 Simulated population per neutron capture calculated by the statistical model versus the normalized experimental cross sections for levels below 900 keV in 186W(n,γ)187W. The Enhanced Generalized Lorentzian (EGLO) photon strength function together with the Back-Shifted Fermi Gas (BSFG) level density model combinations have been used in the statistical analysis; see Ref. [Hur14] for more details. In (a) poor agreement is revealed assuming Jπ assignments of 7/2+ and 11/2+ for the 884.1- and 410.1-keV levels, respectively. Much better agreement is attained in (b) whereupon these assignments are changed to 5/2+ and 9/2+ for the 884.1- and 410.1-keV levels, respectively. Taken from Ref. [Hur14].
Improving nuclear structure data (II): Wavefunction composition
Given sufficient auxiliary information, it is sometimes possible to explore the wavefunction composition of low-lying levels in a nucleus through the (n,γ) reaction. In our recent 139La(n,γ) measurement [Hur19], we were able to assess the tentatively-assigned Jpi = (5-, 6-) level at 322.1 keV in 140La [Nic18]. Systematics in the A ≈ 140 region suggest the levels below ~600 keV are well understood in terms of configurations based on couplings involving the 1g7/2 and 2d5/2 quasiprotons with the 2f7/2 and, to a lesser extent, the 3p3/2 quasineutrons. The fact that all measured angular distributions to levels below 600 keV in 140La are consistent with an orbital angular momentum l = 3 transfer further demonstrates the dominance of the ν(2f7/2) orbital at low excitation; l = 1 transfers indicating the onset of the ν(3p3/2) orbital occur at higher excitation energies [Ker67]. Accordingly, there are 14 low-lying levels expected from the two configurations based on couplings with the 2f7/2 quasineutron:
$$ |\pi(1g_{7/2}) \otimes \nu(2f_{7/2}); J^{\pi} = 0^{-},1^{-},2^{-},3^{-},4^{-},5^{-},6^{-},7^{-} \rangle \\ |\pi(2d_{5/2}) \otimes \nu(2f_{7/2}); J^{\pi} = 1^{-},2^{-},3^{-},4^{-},5^{-},6^{-} \rangle $$Because, two Jπ = 5- assignments are already assigned to the lower-lying levels at 34.6 and 103.8 keV, this leaves a Jπ = 6- assignment as the only remaining possibility from the above octuplet and sextuplet of levels, with the other 6- assignment occupied by the 48.9-keV level. Particle-phonon coupling is demonstrably insignificant at such low excitation energies in 140La [Jur70], and given the observed energy regime of l = 1 transfers, the ν(3p3/2) orbital is unlikely to play an important role through four-quasiparticle admixtures in the vicinity of the 322.1-keV level. Furthermore, a 6- level cannot be generated by coupling quasiparticles in the ν(3p3/2) orbital with those in the available proton orbitals. The state vector for this 6- level can, thus, be characterized assuming the mixed configuration:
$$ \alpha^{2}|\pi(1g_{7/2}) \otimes \nu(2f_{7/2}); J^{\pi}=6^{-}\rangle \oplus \beta^{2}|\pi(2d_{5/2}) \otimes \nu(2f_{7/2}); J^{\pi} = 6^{-} \rangle, $$where the mixing amplitudes
$$ \alpha^{2} + \beta^{2} = 1.$$Direct reaction theory shows that the cross section for a state produced in a (d,p) reaction is proportional to its spectroscopic factor (S), thus S ∝ α2 for π(1g7/2) occupancy and S ∝ β2 for π(2d5/2) occupancy. In previous 139La(d,p) work, the authors measure |α| = 1.0 for the 48.9-keV 6- level [Ker67] and do not observe a second 6- level. However, neutron capture reactions, which are generally expected to proceed through the formation of a compound nucleus, are not subject to this selectivity. Accordingly, we propose the observed 322.1-keV level in 140La is the final level of the sextuplet to be accounted for with Jπ = 6- corresponding to an essentially pure π(2d5/2) quasiproton (β=|1.0|) configuration:
$$ |\pi(2d_{5/2}) \otimes \nu(2f_{7/2}); J^{\pi} = 6^{-} \rangle. $$Improving nuclear structure data (III): Neutron-separation energy
The neutron-separation energy Sn defines the threshold at which the nucleus becomes unbound due to emission of a neutron, whereupon the difference in binding energy (Bn) between two neighbouring nuclei vanishes:
$$ S_{n}(Z,N) = B_{n}(Z,N) - B_{n}(Z,N-1) = 0. $$Analysis of primary γ rays (i.e., those that originate at the separation energy) observed in radiative thermal neutron capture is demonstrably successful [Hur14, Hur15, Mat16, Hur19] in its application for the determination of this quantity in accordance with
$$ S_{n} = E_{\gamma} + E_{f} + E_{r}, $$where Eγ is the primary γ-ray energy, Ef is the associated final level of the transition, and Er = Eγ2/2A is the nuclear-recoil energy. Although Sn is frequently well measured, thermal (n,γ) measurements provide an independent verification of this quantity, often with improved uncertainty. However, there remain cases where Sn is poorly known still. For example, until recently Sn for 181W was rather imprecise with a reported value of 6686(5) keV [Wan12]. The compound nucleus 181W may be formed following radiative neutron capture onto 180W. Because 180W is formed in p-process nucleosynthesis (through a series of photodisintegration (γ,n) reactions from s-process seeds during shockwave passage in the neon-oxygen shells in Type-II supernovae [Woo78, Rau02]), it has a very low natural abundance of only 0.12%. This low abundance makes it difficult to work with experimentally, however, given that there are so few stable nuclei available for p-process studies, new measurements to help improve or verify the quality of data are often needed. From our recent work on 180W(n,γ) [Hur15], using a sample enriched to 11.35% in 180W, we determined a new value n = 6669.02(16) keV based on the primary γ-ray analysis shown in Fig. 3, where several new transitions from the 1/2+ capture state to 1/2- and 3/2- states were identified. This new value is significantly different (more than 3 standard deviations) to the previous value [Wan12] and represents an order of magnitude improvement in uncertainty. Our result for Sn has since been adopted into the current Atomic Mass Evaluation AME2016 [Wan17].
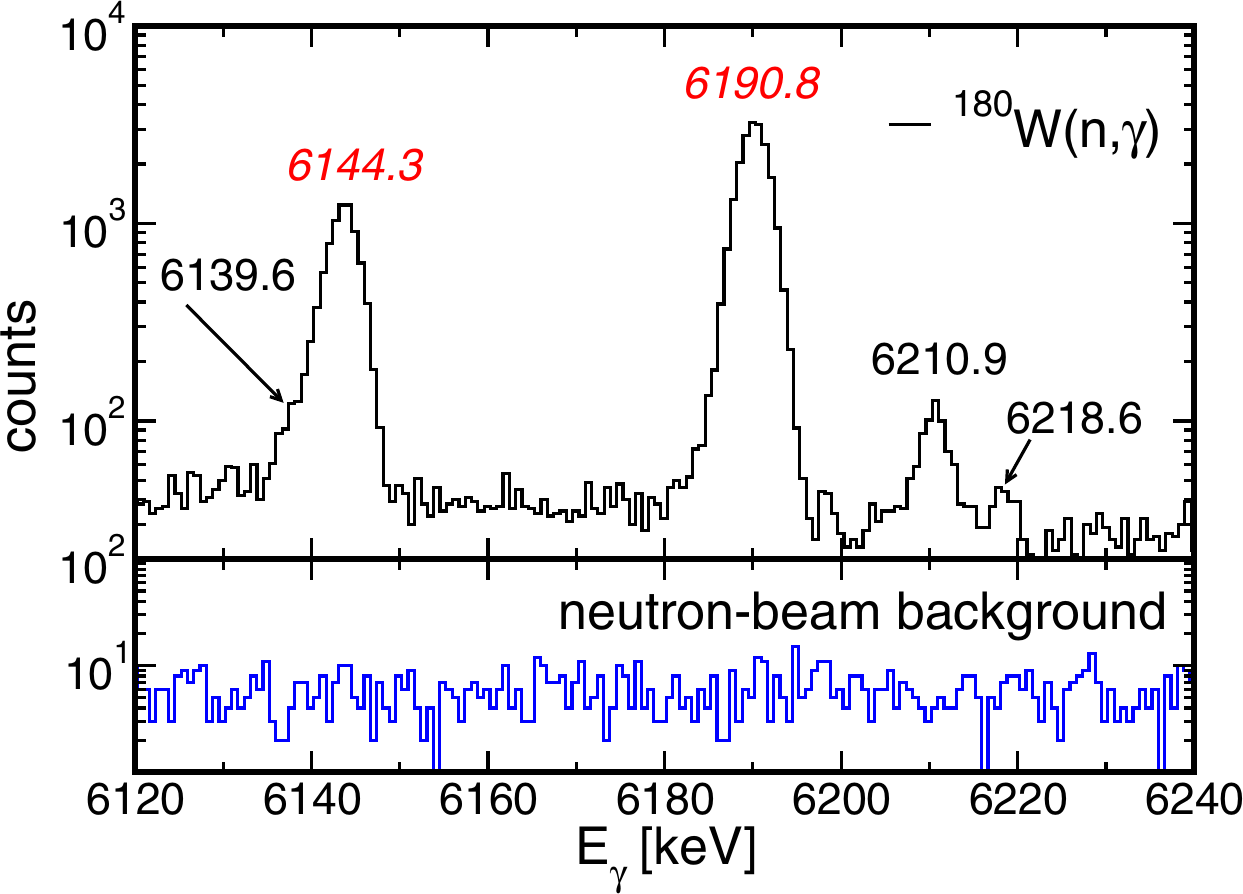
Figure 3 The upper panel shows the spectrum of primary γ rays originating at Sn in 181W from the 180W(n,γ) reaction; the lower panel shows the background spectrum over the same energy region produced by the neutron beam. New transitions in 181W, identified in this work, are labeled in black (6139.6, 6210.9, and 6218.6 keV), while the transitions labeled in red (6144.3 and 6190.8 keV) correspond to contaminant lines from the 182W(n,γ) reaction. Taken from Ref. [Hur15].
Student Alumni
In recent years several students have worked with our program on radiative neutron-capture projects. Their work has led partial or complete fulfillment of their thesis requirements, in addition to publication of their work in peer-reviewed journals. A summary of the students involved and their accomplishments is presented below.

DAVID MATTERS graduated with his Ph.D. in Applied Physics from the Air Force Institute of Technology in 2016, and he now serves as a senior program manager in the NNSA's Defense Nuclear Nonproliferation office of Research and Development (NA-22). His dissertation research was focused on the nuclear structure of 186Re, informed by several reactions including thermal-neutron capture on 185Re. David's portfolio at NA-22 includes nuclear emergency response and arms control verification and monitoring R&D, and he also serves as a point of contact for nuclear data projects related to proliferation detection. David published his work on 185Re(n,γ) in Physical Review C. Link to David's thesis. Berkeley Nuclear Data Program mentor: Dr. Aaron Hurst

ANDREW LERCH Lieutenant Colonel (LTC) Andrew Lerch (Army) performed radiative thermal neutron-capture cross-section measurements on the 185Re nucleus following irradiation of a highly-enriched target at the Budapest Research Reactor to examine the nuclear-structure properties of the residual nucleus 186Re. The body of work included a consortium of researchers from the U.S. Department of Defense (Army Research Laboratory and Air Force Institute of Technology), Department of Energy laboratories, universities, and allied partners. LTC Lerch specializes in nuclear survivability test & evaluation of radiation-hardened microelectronics for strategic, space, and ballistic missile defense systems. He is currently assigned to the United States Space Force staff at the Pentagon as the Strategic Synchronization Branch Chief. Previously, he served in the United States Army Nuclear and Countering Weapons of Mass Destruction Agency; the Office of the Assistant Secretary of Defense for Nuclear, Chemical, and Biological Defense Programs; and the Defense Threat Reduction Agency. Andrew published his work on 185Re(n,γ) in Physical Review C. Link to Andrew's thesis. Berkeley Nuclear Data Program mentor: Dr. Aaron Hurst

CHRISTOPH GENREITH graduated with a Ph.D. in Nuclear Physics from Forschungszentrum Jülich in Germany. His research focused on cold-neutron prompt-gamma activation analysis of actinides at the FRM-II (Forschungs-Neutronenquelle Heinz-Maier-Leibnitz) research reactor in Garching, Germany. During the Fall of 2014, Christoph joined the Lawrence Berkeley National Laboratory as a Visiting Scholar whereupon he carried out the analysis of the 242Pu(n,γ) measurements. After graduation, Christoph continued Postdoctoral research at the FRM-II prior to embarking upon a law career as a European patent attorney. Christoph published his work on 242Pu(n,γ) in the Journal of Radioanalytical and Nuclear Chemistry. Link to Christoph's thesis. Berkeley Nuclear Data Program mentors: Dr. Rick Firestone and Dr. Aaron Hurst

DANYAL TURKOGLU obtained his Ph. D. in Nuclear Engineering from The Ohio State University in 2014. He is currently a Nuclear Engineer at the National Institute of Standards and Technology (NIST) in Gaithersburg, Maryland. During his time in Berkeley, Danyal worked on the prompt gamma activation analysis of 93Nb thermal-capture data. Danyal published his work on 93Nb(n,γ) in the Transactions of the American Nuclear Society. Link to Danyal's thesis. Berkeley Nuclear Data Program mentors: Dr. Shamsuzzoha Basunia and Dr. Aaron Hurst

ADRIANA SWEET began working with the Nuclear Data Program through the Nuclear Science and Security Consortium (NSSC) as an undergraduate in the Department of Nuclear Engineering at UC Berkeley. Her contributions to the modeling and analysis of the 139La(n,γ) data were recognized recently as the recipient of a departmental award for her achievements. In the Summer of 2020 Adriana received her Ph. D. in the Department of Nuclear Engineering at UC Berkeley. Adriana's thesis topic on low-energy nuclear physics related to level density and photon strength studies of neutron-rich nuclei provided the first experimentally-deduced neutron-capture cross section for radioactive 92Sr using the β-Oslo Method. Dr. Adriana Sweet is currently a Postdoctoral Research Fellow at the Lawrence Livermore National Laboratory. Adriana published her work on 139La(n,γ) in Physical Review C. Berkeley Nuclear Data Program mentors: Dr. Aaron Hurst, Dr. Bethany Goldblum, and Prof. Lee Bernstein.
References
[Hur17] A.M. Hurst et al., "Developments in capture-γ libraries for nonproliferation applications", Eur. Phys. J. Web of Conf. 146, 09008 (2017). [Hur19] A.M. Hurst, A. Sweet et al., "Radiative-capture cross sections for the 139La(n,γ) reaction using thermal neutrons and structural properties of 140La", Phys. Rev. C 99, 024310 (2019). [Hur15] A.M. Hurst et al., "Radiative thermal neutron-capture cross sections for the 180W(n,γ) reaction and determination of the neutron-separation energy, Phys. Rev. C 92, 034615 (2015). [Hur14] A.M. Hurst et al., "Investigation of the tungsten isotopes via thermal neutron capture", Phys. Rev. C 89, 014606 (2014). [Mat16] D.A. Matters, A.G. Lerch, A.M. Hurst et al., "Investigation of 186Re via radiative thermal-neutron capture on 185Re", Phys. Rev. C 93, 054319 (2016). [Hur15b] A.M. Hurst et al., "Determination of the effective sample thickness via radiative capture", Nucl. Instrum. Methods Phys. Res. Sect. B 362, 38 (2015). [Xmu98] XMuDat, Photon attenuation data on PC, version 1.0.1, 1998. [Ber12] J. Beringer et al. (Particle Data Group), Phys. Rev. D 86, 010001 (2012), G. Cowan, Statistics, p. 390. [War21] T. Warren et al., "Prompt γ-activation analysis of 188Re", manuscript in preparation. [Bas09] M.S. Basunia, Nucl. Data Sheets 110, 999 (2009). [Nic18] N. Nica, Nucl. Data Sheets 154, 1 (2018). [Ker67] J. Kern, G.L. Struble, and R.K. Sheline, Phys. Rev. 153, 1331 (1967). [Jur70] E.T. Jurney et al., Phys. Rev. C 2, 2323 (1970). [Wan12] M. Wang et al., Chin. Phys. C 36, 1603 (2012). [Woo78] S.E. Woosley and W.M. Howard, Astrophys. J. Suppl. 36, 285 (1978). [Rau02] T. Rauscher et al., Astrophys. J. 576, 323 (2002). [Wan17] M. Wang et al., Chin. Phys. C 41, 030003 (2017).